会社の成長と株式価値（後編）
〜 ROE を用いたモデル 〜

（1999.03.02）


最近，ROE（return on equity，株主資本利益率）を重視する投資家や経営者が増えてきました．今回は，「ROE とは何ぞや？」というところから始めて，ROE を用いて株式の投資価値計算を行い，「なぜ ROE が重要視されるのか？」「どういう投資姿勢で挑むとき，ROE は重要なのか？」「ROE に応じ，株主還元策はどうあるべきか？」ということなどを考えて行きまーす．

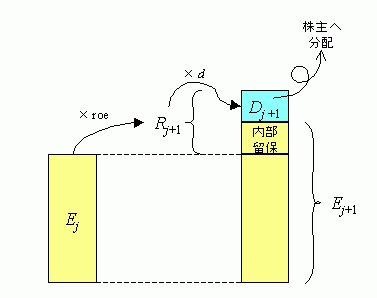
まず，ROE は，1 営業期間の期初の資本とその期間の利益（税引後純利益）とを用いて，

ROE ＝ 利益 ／ 資本

と定義されます．したがって，

ROE ＝ 1 株利益 ／ 1 株純資産

でもあります．ここで，1 株純資産は，会社の資産のうち株主の持分を 1 株当りに換算したものです．また，1 株利益は，会社が 1 営業年度で稼ぎ出した付加価値のうち株主の取分（役員賞与金込み）を 1 株当りに換算したものです．したがって，株主の立場から見ると，ROE は，株主の持分をどの程度の効率で運用できたかを示しています．これが，投資家達に重視される理由でもあります．預金者が預金利率を重視するのと似ています．

ROE が資本の運用効率を表すということで，新聞・経済誌の解説記事などで，「A 社は，ROE が 10% であり，3〜5% 程度の同業他社に比べ資本効率が良い．」というような記述が良く見られます．しかし，これで終わっちゃー，あまりにもモッタイナイ．ガムを 1 回だけ噛んで捨ててしまうようなものです．

ROE がモッタイナイ

以下では，ROE を株式の投資価値計算に持込んで，その重要性を検証してみましょう．
さっそく問題提示します．配当落ち直後（配当金が支払われた直後）の株式があり，1 株純資産が 10 万円，ROE が毎年一定で 20%，配当性向（利益のうち配当金に回す額の割合）が毎年一定で 50% とします．12 年後の配当落ち直後，その会社は解散し，残余財産（残った資本）は簿価通り持株数に応じて株主に分配されるものとします．その株式の現在の投資価値は，配当落ち直後で，幾らと計算されるべきでしょう？ただし，役員賞与は考えない（利益は，配当金と内部留保とに分配される）ものとし，一般的な債券・預貯金の類で 1 年間お金を運用したときの利子率は 3% で，これもまた毎年一定とします．

またまた，数学になっちゃいましたあ．しかも，計算がちと複雑そうです．目まいがします．
実は，この問題は，10 万円，20%，50%，12 年，3% といった具体的数字で計算すると，頭が爆発します．ここでは，最初の配当落ち直後の時点を第 0 期末とし，j ＝ 0，1，2，・・・として，

roe ： 1 営業期間（1 年とは限らない）の ROE， roe ≧ 0 （赤字は論外），
d ： 配当性向， 0 ≦ d ≦ 1，
r ： 1 営業期間の利子率， r ＞ 0，
Ej ： 第 j 期末の 1 株純資産， E0 ≧ 0 （債務超過は論外），
Rj ： 第 j 期の 1 株利益，
Dj ： 第 j 期末の 1 株当り配当金

と置き一般化しちゃって，この文字モジ君達の間に成立つ関係

R，D，E の関係

Rj＋1 ＝ roe・Ej ，
Dj＋1 ＝ d Rj＋1 ，
Ej＋1 ＝ Ej ＋ （Rj＋1 − Dj＋1）

を整理します．すると，k ＝ 1，2，3，・・・として，

Ek ＝ E0｛1 ＋ roe・（1 − d ）｝k，
Dk ＝ E0・roe・d ｛1 ＋ roe・（1 − d ）｝k-1

となりやんす．ここまで来りゃあ，あと一歩か二歩．解散するのが n （＝ 1，2，3，・・・） 期後として，投資価値 Vn は，D1，D2，・・・，Dn と En とを現在価値（→ 「株式投資入門第 4 話：株式の市場価格と投資価値」）に割引いて足し合せりゃいいんです．

Vn ＝
D1
1 ＋ r		 ＋ D2
(1 ＋ r)2		 ＋ ・・・ ＋ Dn
(1 ＋ r)n		 ＋ En
(1 ＋ r)n
＝
E0 { roe・d/
1 ＋ r		 ( 1 ＋ c ＋ ・・・ ＋ cn-1 ) ＋ cn }．

ただし，

c ＝ 1 ＋ roe・（1 − d ）
1 ＋ r		 ．

Vn の式をさらに整理すると，

  • 0 ＜ c ＜ 1，1 ＜ c の場合
Vn ＝ E0 ( roe・d/
1 ＋ r		 ・ cn − 1
c − 1		 ＋ cn )，
  • c ＝ 1 の場合
    Vn ＝ E0 ( n・roe・ d/
    1 ＋ r    		 ＋ 1 )．

    ほ〜らほら，尤もらしくて訳の解らない式が出てきたでしょう．これで一般式は完成．ここからは，「どんな奴でも掛かってきやがれ．うりゃー！」という訳で，先程の具体的数字：

    roe ＝ 20%，
    d ＝ 50%，
    r ＝ 3%，
    E0 ＝ 10 万円，
    n ＝ 12 年

    を代入してみると，

    V12 ＝ 10・ ( 0.20・0.50/
    1.03    		 ・ (1.10 ／ 1.03)12 − 1
    (1.10 ／ 1.03) − 1    		 ＋ (1.10 ／ 1.03)12 ) ＝ 39.17（万円）．

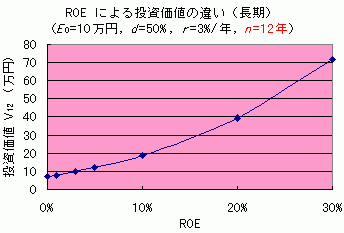
    もう，ついでだから，いろいろ代入しちゃいます．ROE を変化させて投資価値 V12 を計算した結果が，次のグラフです．V12 は ROE の 12 次関数なので，ROE 増加に応じた V12 の増加の速さは，右に行くほど急になります．高 ROE を長期間持続するような会社の投資価値は，ムチャクチャ高いのです．

    ROE による投資価値の違い（長期）

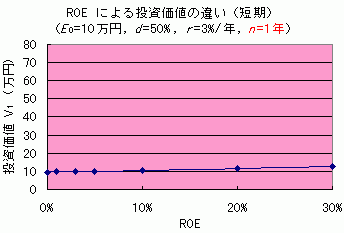
    次のグラフは，n ＝ 1 として，ROE を変化させて投資価値 V1 を計算したものです．V1 は ROE の 1 次関数なので，ROE 増加に応じた V1 の増加の速さは，どっちゅーことありません．いくら高 ROE といっても短期持続じゃあ，会社の投資価値はそれほど高くならないのです．

    ROE による投資価値の違い（短期）

    もうお分かりですね．

    のです．したがって，ROE は，長期投資派にとっては大変重要な指標と言えるでしょう．

    さて，お次のグラフ達は，それぞれ ROE を高めの 20 %，低めの 1% に固定して，配当性向 d を変化させて投資価値 V12 を計算した結果です．縦軸のスケールが違うから気を付けてネ．

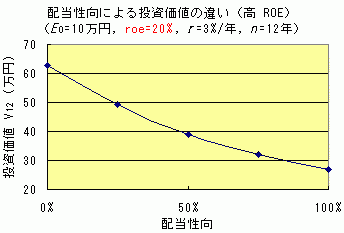
    配当性向による投資価値の違い（高 ROE）

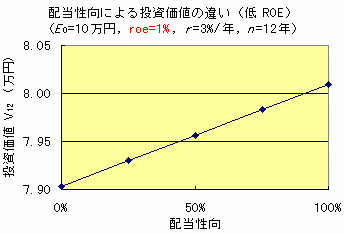
    配当性向による投資価値の違い（低 ROE）

    両グラフは，単調減少・単調増加という好対照な結果を示してます．そう，

    のです．株主は，成長期のうちは低配当に甘んじて内部留保を多くして会社をドンドン太らせ，成熟期に入ったら高配当を吐き出させ，場合によっては会社を解散させる，という姿勢を取るべきなのです．

    以上で，最初に掲げた Question の答えは出尽くしました．こっからはオマケ．ちょっと不思議の国のアリスしましょう．
    今まで使って来た投資価値 Vn の式は，会社が n 期後に解散するという仮定の下に求めたものでした．しかし，現実の会社のほとんどは，永久存続を前提としています．そこで，解散時期を無限期間後へ追いやり，投資価値 V∞ を計算してみます．

    これを整理すると，なんと！

    そう，

    なのです．上の条件式中の roe・（1 − d ） は，内部留保による資本増加率を意味します．この資本増加率が利子率に比べて大きい会社の場合，株価はナンボ高くなっても不思議ではない，ということになります．

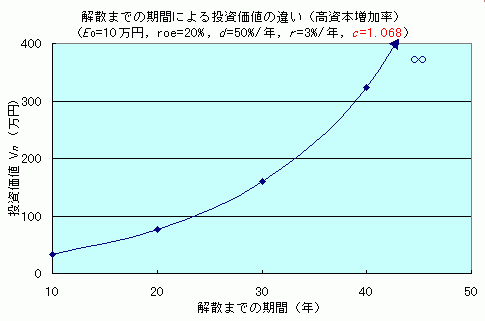
    解散までの期間による投資価値の違い（高資本増加率）

    ときたま，実際の株式市場で，高成長企業の株価が，1 株当りの純資産価値・収益還元価値に比べて，ムチャクチャ高くなることがあります．投資家達は，上のような事情を察知してるんでしょうか・・・（ホントかあ？）
    ホーム
    ホームへ帰る