次に,2 つ目,配当割引法について.お金に絡んだ株主権で,最重要なもののもう 1 つと言えば,利益配当請求権.「株主は,利益の配当を請求できるんだ!」という権利です.すると,配当金額から投資価値を導くことができます.これは,正直言って,理解も説明もちと骨が折れます (^_^;). でも,頑張っちゃいましょう.まずは一例から.(株)ユニシロの利益処分計算書に登場してもらいましょう.Come on!

発行済株式数は 600 株でした.すると,
| 1 年当り 1 株配当金 |
= |
|
|
|
= |
|
|
|
= |
20 千円/(株・年) |
です.ここで,一つの仮定というか予想をしましょう.(株)ユニシロが今後永遠に 20 千円/(株・年)の配当を続けるものと予想します.この株式の投資価値は,配当落ち直後(配当金が支払われた直後)で,幾らと計算されるべきでしょう?ただし,配当金支払日はキッカリ 1 年おきで,一般的な債券・預貯金の類で 1 年間お金を運用したときの利子率は今後永遠に 4% であると予想します.
何だか数学の問題っぽくなっちゃいましたね.そう,実は数学の問題なのです.数学というと苦い思い出をお持ちの方も多いことでしょう.クミヤくんもその一人です.だいたい,あの数学のセンコーが (-∧-#)・・・失礼,熱くなっちゃいました m( _ _ )m.先へ進みましょう.
まずは,手始めに,1 年後(最初)に支払われる 1 株配当金 20 千円の現在価値 V1 を計算しましょう.現在価値を計算するというのは,将来受取る現金等を現在の金額に換算することです.これは,次のように考えます.現在もし現在価値 V1 を一般的な債券・預貯金の類で運用すると,1 年後には 4% 増えて V1 × 1.04 の金融資産を手にすることができます.これが 20 千円になるはず.ちゅーことは,
V1 × 1.04 = 20 千円/株
です.そんでもって,上式の両辺を 1.04 で割ってやれば,
です.ヤッター.取り敢えず,1 年後が完了.じゃあ,2 年後に支払われる配当金 20 千円の現在価値は?これは,さっきの計算の延長戦みたいなもんで,次のように考えます.現在もし現在価値 V2 を一般的な債券・預貯金の類で運用すると,1 年後には 4% 増えて,さらにもう 1 年後には複利で 4% 増えて,結局,今から 2 年後には V2 × 1.04 × 1.04 の金融資産を手にすることができます.これがやっぱり 20 千円になるはず.ちゅーことは,
V2 × 1.042 = 20 千円/株
です.そんでもって,上式の両辺を 1.042 で割ってやれば,
です.ヤッター2.ついに,2 年後も完了.じゃあ2,3 年後に支払われる配当金 20 千円の現在価値は?もうお分かりですね.
です.やったー3.だんだんクドくなって来たので,一挙に投資価値 V の計算に移りましょう.この V は,1 年後,2 年後,3 年後,・・・に支払われる配当金の現在価値の列 V1,V2,V3,・・・の総和として求めれば OK です.Let's go!
| V |
= |
V1+V2+V3+・・・ |
|
|
= |
20 千円/株
1.04 |
+ |
20 千円/株
1.042 |
+ |
20 千円/株
1.043 |
・・・ |
|
|
= |
500 千円/株 |
ハイ,一例オシマイ.以上のように,毎年の配当金を現在価値に割引いて足し合せるところに,配当割引法という名前の由来があります.
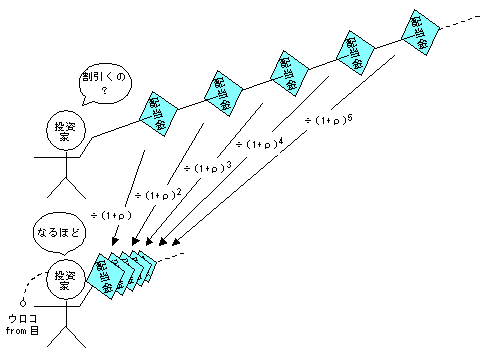
ところで,お気づきでしたか?先の計算で,
20 千円/株
1.04 |
+ |
20 千円/株
1.042 |
+ |
20 千円/株
1.043 |
・・・ |
= |
500 千円/株 |
の部分には,論理の飛躍があります.実は,こっそりと等比級数の和の公式:
| a + a r + a r 2 +・・・ |
= |
a
1−r |
(ただし,|r| < 1) |
を使っていたのです.これは,クミヤくんの場合,高校 3 年生くらいの微分積分学で習った気がします.(-_-)zzz 居眠りしてたのでほとんど記憶にありませんが.まあ,公式を信用して,そのまま使っちゃえばいいでしょう.
ところで,今まで,20 千円/(株・年) とか年利子率 4% とか具体的な数字をあてはめて配当割引法の計算をしてました.せっかくなので,一般化しちゃいましょう.それには,配当金支払時期を 1 年おきとは限らずに一定期間毎として,その一定期間を 1 期として,1 期 1 株当り配当金予想を一定額 d (≧ 0)として,更に 1 期当り利子率予想を一定値 ρ (> 0)とします.すると,
| 1 株当り配当割引価値 |
= |
d
1 + ρ |
+ |
d
(1 + ρ)2 |
+ |
d
(1 + ρ)3 |
+ |
・・・ |
|
|
|
|
|
= |
|
|
|
= |
|
です.これを株式の投資価値と見なせます.ハイ,これでオシマイ.どう?導くのは複雑でも,最後は簡単でしょう.
なお,利子率予想についてですが,「実際,何の利子率を使うの?普通預金?定期預金?社債?国債?・・・」という疑問をお持ちの方も多いでしょう.先の式を計算の仮定で「永遠に・・・」とか言っていることを考えると,長期債に関する利子率を使うのが妥当でしょう.クミヤくんの場合,日経公社債インデックス長期債っちゅーのを使っています.これは,長期公社債(国債や社債などで償還までの残存期間が 7 年以上のもの)の平均利回りです.日経新聞に毎日最新の値が掲載されるので,けっこう便利です.
さてと,3 つ目,収益還元価値法について.残余財産分配請求権と利益配当請求権,これら 2 つを合せると,「配当金だけじゃない.当期純利益総てが株主のもんだ!」という考え方に至ります.すると,当期純利益額から投資価値を導くことができます.それには,ある一定期間を 1 期として,1 期 1 株当り当期純利益予想を一定額(≧ 0)として,更に 1 期当り利子率予想を一定値(> 0)として,計算に移るのが本筋です.が,皆さんお察しの通り,計算は,配当割引法の 1 期 1 株当り配当金予想のところを 1 期 1 株当り当期純利益予想で置き換えるだけのことで,
| 1 株当り収益還元価値 |
= |
1 期 1 株当り当期純利益予想
1 期当り利子率予想 |
|
|
|
= |
1 期当り当期純利益予想
発行済株式数 × 1 期当り利子率予想 |
|
です.ここで一例.(株)ユニシロの損益計算書に登場してもらいましょう.Come on!

この当期純利益 27,000 千円が,今後も永遠に毎期続くものと予想します.発行済株式数は 600 株でした.1 期当り利子率予想はやはり 4% であるとします.すると,
| 1 株当り収益還元価値 |
= |
1 期当り当期純利益予想
発行済株式数 × 1 期当り利子率予想 |
|
|
|
= |
|
|
|
= |
1,125 千円/株 |
と計算できちゃいます.結局,簡単でしょ.
いよいよ,最後の 4 つ目,折衷法について.先の純資産法,配当割引法,収益還元価値法を較べてみると,けっこう投資価値がバラついているのが判ります.となると,「どの方法で投資価値を計算したらいいの?」なんて迷いも生じます.そこで,頭に浮かぶのは,3 つ足して 3 で割るみたいな妥協案です.もうちょっと一般的に考えると,
| 1 株当り折衷投資価値 |
= |
1 株当り純資産価値 × (1 − α − β) + |
|
|
|
1 株当り配当割引価値 × α + |
|
|
|
1 株当り収益還元価値 × β |
|
|
(α,β は,0≦α,0≦β,α+β≦1 の範囲で適当に選ぶ.)
|
です.ここで,α=β=0 なら純資産法,α=1,β=0 なら配当割引法,,α=0,β=1 なら収益還元価値法と一緒で,それら以外なら正に 2〜3 法の折衷法,妥協の産物となります.この方法は,「俺ってさあ,収益還元価値法が好きなんだけどぉ,でも,純資産法,配当割引法も捨て難いしなあ.優柔不断なのよ」みたいなときに便利です.α,β をどう選ぶか,これは各投資家の判断に委ねられます.
ここで,またまた(株)ユニシロの例に再登場してもらいましょう.確か,
| 1 株当り純資産価値 |
= |
400 千円/株 |
, |
|
| 1 株当り配当割引価値 |
= |
500 千円/株 |
, |
|
| 1 株当り収益還元価値 |
= |
1,125 千円/株 |
|
でした.試しに,先ほどの折衷法の式で α=0.3,β=0.6 として計算してみると,
| 1 株当り折衷投資価値 |
= |
1 株当り純資産価値 × (1 − α − β) + 1 株当り配当割引価値 × α + 1 株当り収益還元価値 × β |
|
|
= |
400 千円/株 × 0.1 + 500 千円/株 × 0.3 + 1,125 千円/株 × 0.6 |
|
|
= |
865 千円/株 |
です.う〜ん,確かに,400 千円/株,500 千円/株,1,125 千円/株の間を行くマイルドな値.ちょー心地イイ〜.
さて,投資価値計算法が解ったところで,次回は,経営破綻しなさそうな投資先を選ぶために,安全性の財務分析について考えてみましょう.
